Maple Colle XV
> restart;
> with(linalg):
Warning, the protected names norm and
trace have been redefined and unprotected
> A:=matrix(2,2,[1,2,0,1]);
![]()
> B:=evalm(1/sqrt(2)*matrix(2,2,[1,1,1,-1]));
![B :=
matrix([[1/2*sqrt(2), 1/2*sqrt(2)], [1/2*sqrt(...](images/15collemaple2.gif)
> C:=evalm(1/25*matrix(3,3,[-16,12,-15,12,-9,-20,15,20,0]));
![C :=
matrix([[-16/25, 12/25, -3/5], [12/25, -9/25, ...](images/15collemaple3.gif)
> DD:=matrix(3,3,[1/2+sqrt(3)/4 , sqrt(2)/4 , 1/2-sqrt(3)/4 , -sqrt(2)/4, sqrt(3)/2, sqrt(2)/4, 1/2-sqrt(3)/4 , -sqrt(2)/4 , 1/2+sqrt(3)/4]);
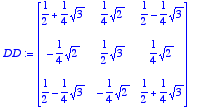
XVI.1
>
isométrie:=proc(M::matrix)
local tMM,Id,n,m;
tMM:=evalm(transpose(M)&*M);
tMM:=map(simplify,tMM);
# On voit en effet sur l'exemple de la matrice DD que les coefficients ont
besoin d'être simplifiés
n:=rowdim(M);m:=coldim(M);
Id:=diag(1$n);
if n<>m then "Il faut au moins que la matrice soit carrée !"
elif not(equal(tMM,Id)) then "Ce n'est pas une isométrie"
elif det(M)=1 then "C'est une isométrie directe"
else "C'est une isométrie indirecte"
fi;
end:
> isométrie(A);
![]()
> isométrie(B);
![]()
> isométrie(C);
![]()
> isométrie(DD);
![]()
> isométrie(matrix([[1,2,3]]));
![]()
>
XVI.2
>
axe:=proc(M::matrix)
if isométrie(M)<>"C'est une isométrie indirecte" or
rowdim(M)<>2
then "Erreur, ce n'est pas une matrice de réflexion plane"
else kernel(M-1)
fi;
end:
> axe(A);
![]()
> axe(B);
![]()
>
>
réflexion2:=proc(V::vector)
local e1,e2,x1,x2,P,R;
e1:=evalm(1/norm(V,2)*V);
# On rend V unitaire
x1:=e1[1];x2:=e1[2];
e2:=vector([-x2,x1]);
# On construit le vecteur directement orthogonal à e1
P:=concat(e1,e2);
# Matrice de passage de la base canonique vers (e1,e2)
R:=matrix(2,2,[1,0,0,-1]);
# Matrice de la réflexion dans la base (e1,e2)
evalm(P&*R&*inverse(P));
end:
> v:=vector([-2,5]): réflexion2(v);
![matrix([[-21/29, -20/29], [-20/29, 21/29]])](images/15collemaple12.gif)
>
XVI.3
> w:=vector([1,-1,1]);
![]()
> w0:=evalm(1/norm(w,2)*w);
![]()
> u:=vector([1,0,-1]);
![]()
> u0:=evalm(1/norm(u,2)*u);
![]()
> v0:=crossprod(w0,u0);
![]()
> P:=concat(u0,v0,w0);
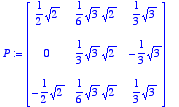
> # P est la matrice de passage de la base canonique vers la base orthonormale (u0,v0,w0);
> S0:=diag(1,1,-1);
![S0 :=
matrix([[1, 0, 0], [0, 1, 0], [0, 0, -1]])](images/15collemaple19.gif)
> # S0 est la matrice de la réflexion dans la base (u0,v0,w0);
> S:=evalm(P&*S0&*transpose(P));
![S :=
matrix([[1/3, 2/3, -2/3], [2/3, 1/3, 2/3], [-2...](images/15collemaple20.gif)
> isométrie(S);
![]()
> R0:=matrix(3,3,[cos(t),-sin(t),0,sin(t),cos(t),0,0,0,1]);
![R0 :=
matrix([[cos(t), -sin(t), 0], [sin(t), cos(t)...](images/15collemaple22.gif)
> R:=evalm(P&*R0&*transpose(P)):
> RPi_2:=subs(t=Pi/2,evalm(R)):
> map(simplify,RPi_2);
![matrix([[1/3, -1/3*sqrt(3)-1/3, -1/3*sqrt(3)+1/3], ...](images/15collemaple23.gif)
> RPi_6:=subs(t=Pi/6,evalm(R)):
> map(simplify,RPi_6);
![matrix([[1/3*sqrt(3)+1/3, -1/3, -1/3*sqrt(3)+1/3], ...](images/15collemaple24.gif)
> isométrie(RPi_6);
![]()
>
XVI.4
Étude de C
> isométrie(C);
![]()
Ainsi C est une réflexion ou une composée rotation réflexion. Cherchons les invariants.
> Inv:=kernel(C-1);
![]()
Donc C est une composée rotation réflexion, l'axe de la rotation étant orthogonal au plan de la réflexion. Cherchons les vecteurs changés en leurs opposé (ceux de l'axe de la rotation)
> Opp:=kernel(C+1);
![]()
> w:=op(Opp):w0:=evalm(1/norm(w,2)*w);
![]()
On choisit un vecteur unitaire orthogonal à w0. En orientant l'axe par w0, l'angle de la rotation est donné par les formules classiques (accompagnées d'une figure)
> u0:=vector([0,0,1]);
![]()
> v0:=crossprod(w0,u0);
![]()
> dotprod(u0,C&*u0);
![]()
Donc le cosinus de l'angle est 0. La rotation est d'angle +/- Pi/2
> dotprod(v0,C&*u0);
![]()
Ainsi C est la matrice de la composée de
la réflexion de plan Vect(u0,v0) (orthogonal à w0)
la rotation d'axe Vect(w0), orienté par w0, d'angle -Pi/2
>
Étude de DD
> isométrie(DD);
![]()
C'est donc la matrice d'une rotation. On en détermine l'axe
> Inv:=kernel(DD-1);
![]()
> w:=op(Inv):w0:=evalm(1/norm(w,2)*w);
![]()
On oriente l'axe Vect(w0) par w0 et on choisit un vecteur unitaire orthogonal à w0.
> u0:=vector([0,1,0]);
![]()
> dotprod(u0,DD&*u0);
![]()
> alpha:=arccos(%);
![]()
On connaît donc le cosinus de l'angle, donc l'angle au signe près. Déterminons le sinus pour en avoir le signe.
> dotprod(crossprod(w0,u0),DD&*u0);
![]()
> alpha:=-alpha;
![]()
Il s'agit donc de la rotation d'axe dirigé et orienté par w0, d'angle -Pi/6
>
>
> restart;
> with(linalg):
Warning, the protected names norm and
trace have been redefined and unprotected
XVI.5
> M:=evalm(a*matrix(3,3,[1,1-b,1+b,1+b,1,1-b,1-b,1+b,1]));
![M :=
matrix([[a, a*(1-b), a*(1+b)], [a*(1+b), a, a*...](images/15collemaple42.gif)
C'est une matrice de rotation si et seulement si elle est orthogonale et son déterminant est +1
> tMM:=evalm(transpose(M)&*M-1);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
M est orthogonale si et ssi cette matrice est nulle. On utilise un ensemble pour éliminer tout de suite les équations en double. À la fin apparait l'équation pour que M soit directe.
> eqs:={seq(seq(tMM[i,j],i=1..3),j=1..3),det(M)-1};
![]()
![]()
> S:=solve(eqs,{a,b});
![]()
> S:=allvalues(S);
![]()
> M1:=subs(S[1],evalm(M));M2:=subs(S[2],evalm(M));
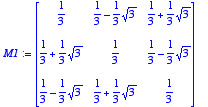
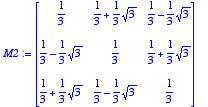
Reste à déterminer les éléments caractéristique des M1 et M2
> w:=op(kernel(M1-1)):w1:=evalm(1/norm(w,2)*w);
![]()
> w:=op(kernel(M2-1)):w2:=evalm(1/norm(w,2)*w);
![]()
Les deux rotations ont le même axe dirigé par w1. On oriente cet axe par w1. On détermine l'angle par la méthode usuelle.
> u:=vector([1,-1,0]):u1:=evalm(1/norm(u,2)*u);
![]()
> v1:=crossprod(w1,u1);
![]()
On note C1, S1 le cosinus et sinus de l'angle de M1, notation analogue pour M2
> C1:=dotprod(u1,M1&*u1);
![]()
> S1:=dotprod(v1,M1&*u1);
![]()
Donc M1 est d'angle +Pi/2 avec notre orientation.
> C2:=dotprod(u1,M2&*u1);
![]()
> S2:=dotprod(v1,M2&*u1);
![]()
Et M2 est d'angle -Pi/2
>
>