XIV.1

> with(linalg):

Warning, the protected names norm and 
trace have been redefined and unprotected

> A:=evalm(matrix(5,5,1)+diag(1$5));

On cherche les lambda pour que A-lambda I_5 ne soit pas inversible (valeurs propres de A)

> solve(det(A-lambda)=0,lambda);

On cherche les noyaux correspondant (espaces propres) par une base (vecteurs propres)

> H6:=kernel(A-6);

> H1:=kernel(A-1);

On écrit la matrice des vecteurs propres. S'ils forment une base de R^5, cette matrice est inversible et c'est la matrice de passage.

> P:=concat(op(H6),op(H1));

> det(P);

Tout va bien. P est inversible, donc la famille des vecteurs propres est une base de R^5. La matrice de f dans cette base est donnée par la formule de changement de base (en réfléchissant une seconde, on comprend et on explique tout de suite le résultat).

> DD:=evalm(P^(-1)&*A&*P);

On fait alors la remarque que DD^n se calcule facilement en élevant à la puissance n chaque coefficient de DD. (C'est bien parce que DD est diagonale que l'on peut dire cela). Pour cela on applique ( map ) la puissance n à chaque coefficient.

> DDn:=map(x->x^n,DD);

On a alors A^n=PDDP^(-1)PDDP^(-1)...PDDP^(-1). Après simplification (récurrence immédiate), on obtient A^n=PDD^nP^(-1)

> An:=evalm(P&*DDn&*P^(-1));

>

> restart;

XIV.2

> ED:=x*(x^2+1)*diff(y(x),x)-(x^2-1)*y(x)=-2*x;

On résout sur R+* et R-* à l'aide de dsolve

> dsolve(ED,y(x));

> assign(%);

> f:=unapply(y(x),x,_C1);

> plot({seq(f(x,C1),C1=-5..5)},x=-10..10,y=-10..10,scaling=constrained);

On cherche à raccorder une solution de paramètre C1 avec une solution de paramètre C2 en 0; Il faut déjà que les fonctions admettent une limite en 0, ce qui n'est le cas que pour C1=-1. Dans ce cas, la fonction est x->-x, qui est dérivalble et satisfait l'ED donc solution sur R.

> tangente:=
y-f(2,C1)=subs(x=2,diff(f(x,C1),x))*(x-2);

> t1:=subs(C1=0,tangente):
t2:=subs(C2=1,tangente):

> solve({t1,t2},{x,y});

> assign(%);

> evalb(tangente);

Ainsi les coordonnées (-4/3,4/3) du point A satisfont les équations de toutes les tangentes.

>

> restart;

XIV.3

> ED:=(1+x^2)*diff(y(x),x)-2*x*y(x)=x^3;

> dsolve(ED,y(x));

> assign(%);

> f:=unapply(y(x),x,_C1);

> solve(f(0,C1)=n,C1);

> g:=unapply(f(x,-1/2+n),x,n);

> plot({seq(g(x,n),n=0..5)},x=-5..5,y=-1..7,scaling=constrained);

>

> restart;

XIV.4

> ED:=x*diff(y(x),x)+(1-x)*y(x)=x*exp(x)/(x^4+1);

> dsolve(ED,y(x));

> assign(%);

> f:=unapply(y(x),x,_C1);

> plot({seq(f(x,k),k=-2..2)},x=-10..10,y=-10..10,scaling=constrained);

Faisons l'étude en 0 :

> series(f(x,C1),x=0,1);

Il est ainsi nécessaire que C1=0 pour avoir une limite finie en 0. Un seul candidat donc :

> f(x,0);

On en vérifie la dérivabilité en 0 à l'aide du DL1

> series(f(x,0),x=0,3);

Pas de problème, sa dérivée est 1/2

> plot(f(x,0),x=-5..5,y=-5..5,scaling=constrained);

>

> restart;

XIV.5

Résolution de l'ED sur R+

> ED1:=x*diff(y1(x),x)+(x-1)*y1(x)=x^3;

> dsolve(ED1,y1(x));

> assign(%);

Résolution de l'ED sur R-

> ED2:=-x*diff(y2(x),x)+(x-1)*y2(x)=x^3;

> dsolve(ED2,y2(x));

> assign(%);

Les solutions définies sur R* sont les fonctions qui coincident avec y1 sur R+ pour une valeur de la constante d'intégration et avec y2 sur R- pour une autre valeur de la constante. D'où l'intérêt de la manipulation suivante :

> y1:=unapply(y1(x),x,_C1);

> y2:=unapply(y2(x),x,_C1);

Ceci va nous permettre de différencier les deux constantes d'intégration

> f:=piecewise(x>0,y1(x,C1),y2(x,C2));

> plot({seq(seq(f(x,C1,C2),C2=-6..6),C1=-3..3)},x=-5..5,y=-5..5, scaling=constrained);

>

On cherche à raccorder de façon continue deux fonctions y1 et y2. Calculons donc les limites :

> limit(y1(x,C1),x=0);

> limit(y2(x,C2),x=0);

> series(y2(x,C2),x=0,1);

Pour qu'il puisse y avoir raccordement continu, il n'y a pas de condition sur C1, mais il faut et il suffit que C2=-6

> C2:=-6:plot({seq(f(x,C1,C2),C1=-3..3)},x=-5..5,y=-5..5, scaling=constrained);C2:='C2':

>

Pour obtenir un raccordement dérivable, on pousse le développement limité à un ordre supérieur pour y2, et on calcule celui pour y1

> series(y1(x,C1),x=0,2);

> series(y2(x,C2),x=0,3);

Pour que le raccordement soit dérivable, il faut et il suffit que les dérivées à droite et à gauche de f en zéro soient égales, c'est-à-dire que 3+1/2*C2=-1+C1, donc C1=1

> C2:=-6:C1:=1:plot(f(x,C1,C2),x=-5..5,y=-5..5,scaling=constrained);

>

> restart;

XV.6

1ère méthode : on calcule brutalement l'intégrale et on discute après

> F:=Int((a*x^4+b*x^2+c)/((x-1)^3*(x+2)^5),x);

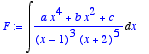
> value(F);

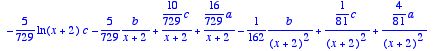
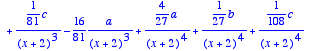
Il faut alors annuler les coefficients devant les termes en ln(x-1) et ln(x-2). On pourrait s'en sortir par une méthode analogue à la fin de la méthode 2.

>

2ème méthode : on décompose d'abord la fraction rationnelle en éléments simples, et on dit a priori les termes qui doivent être nuls (ceux en 1/u uniquement, ici pas de 1/(1+u^2) ou autre).

> f:=(a*x^4+b*x^2+c)/((x-1)^3*(x+2)^5);

> f:=convert(f,parfrac,x);

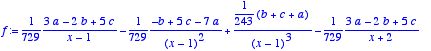
Utilisons un subterfuge pour extraire les termes en 1/(x-1) et 1/(x+2). On va remplacer partout 1/(x-1) par X et 1/(x+2) par Y. On aura alors un polynômes sur lequel on sait extraire les coefficients.

> subterfuge:=subs({x-1=1/X,x+2=1/Y},f);

> eq1:=coeff(subterfuge,X);eq2:=coeff(subterfuge,Y);

> solve({eq1,eq2},{a,b,c});

Bref, l'ensemble des solutions est un e.v. de dimension 2, engendré par (5,0,-3) et (0,5,2).

>

>