Correction des exercices du chapitre XII

> restart;

XII.1

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A1:=matrix(4,4,[0,1,1,1,1,0,-1,-1,1,-1,0,-1,1,-1,-1,0]);

> A2:=matrix([[1,0,1,0],[0,0,0,0],[1,0,0,1],[0,1,0,0]]);

> iA1:=inverse(A1);

> tA2:=transpose(A2);

> equal(transpose(tA2),A2);

> multiply(A1,iA1);

> evalm(3*A1);

> scalarmul(A1,3);

> evalm(A1+A2);

> matadd(A1,A2);

> evalm(A1&*A2);

> multiply(A2,A1);

>

> restart;

XII.2

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> f:=[2*u-v+w,u-3*v+w,5*v-w];

> AA:=genmatrix(f,[u,v,w]);

On obtient ainsi la matrice AA telle que y=f(x) <=> Y=AAX. Ce n'est pas la matrice recherchée~: on veut sa matrice transposée.

> A:=transpose(AA);

> X:=matrix(3,1,[x,y,z]);

> Y:=multiply(A,X);

> noyau:=kernel(A);

> image:=colspace(A);

> restart;

XII.3

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A:=matrix(3,3,[1,-1,1,5,2,-1,3,4,lambda]);

> A1:=addrow(A,1,2,-5);

> A2:=addrow(A1,1,3,-3);

> A3:=addrow(A2,2,3,-1);

> gausselim(A);

Le rang de A dépend de la valeur de lambda. Si lambda=-3, alors le rang est 2. Sinon il est 3.

> rank(A);

> det(A);

> restart;

XII.4

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Définissons la fonction qui à (i,j) associe a(i,j)

> a:=proc(i::integer,j::integer)
if i=j then if i<5 then 1-(1/2)^(5-i)
else 1
fi;
else if i=j+1 then (1/2)^(5-j)
else 0
fi;
fi;
end;

> A:=matrix(5,5);

> for i to 5 do for j to 5 do A[i,j]:=a(i,j) od od:

> evalm(A);

> A2:=matrix(5,5,a); # Avec une fonction d'initialisation.

> V:=matrix(5,1,0):V[1,1]:=1:'V'=evalm(V);

> B:=A:

> for k from 1 to 50 do print([k,multiply(B,V)[5,1]=evalf(multiply(B,V)[5,1])]); B:=B&*A od:

> L:=[]:B:=A:
for k from 1 to 50 do L:=[op(L),[k,evalf(multiply(B,V)[5,1])]]:
B:=B&*A;
od:

> plot(L);

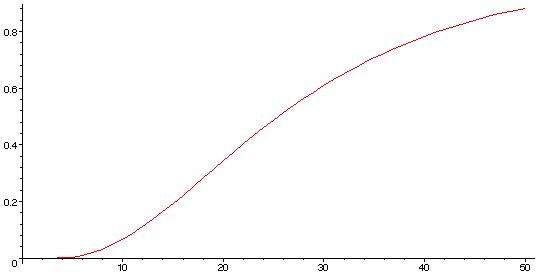
> indice_mini:=proc()
local k,uk;
uk:=multiply(A,matrix(5,1,[1,0,0,0,0])):
for k while(uk[5,1]<0.99 and k<1000) do
uk:=multiply(A,uk);
od;
k;
end;

> indice_mini();

>