Colle d'informatique X
> restart;
X.1
> expr:=(x-3)*(x^2+1)*(1+x);
![]()
> expand(expr);
![]()
> sort(%,x);
![]()
> restart;
X.2
> P:=X^4+2*X^3-4*X^2-5*X-6;
![]()
> factor(P);
![]()
Ceci est la factorisation de Gauss car
![]() n'a pas de racine réelle
n'a pas de racine réelle
> factor(P,complex);
![]()
Remarquons que cette factorisation provoque une recherche numérique.
> factor(P,{I,sqrt(3)});
![]()
C'est la bonne façon de s'en sortir, mais il faut
avoir l'intuition que la factorisation fera intervenir des termes en I et
en
![]() .
.
> restart;
X.3
> A:=n->sin(2*a)*X^n-sin(n*a)*X^2+sin((n-2)*a);
![]()
> B:=X^2-2*cos(a)*X+1;
![]()
Essayons brutalement
> rem(A(n),B,X);
Error, (in quo) arguments must be
polynomial in X
Bien sûr, on pouvait s'attendre à ce que le calcul en soit pas possible : le degré de A dépend de n. Faisons le calcul pour les dix premières valeurs de n
> for k from 1 to 10 do [k,rem(A(k),B,X)] od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cela ne nous dit pas grand chose. Mais on voit que par les formules de trigonométries, le premier reste est nul. Le second l'est aussi. Simplifions les expressions trouvées.
> for k from 1 to 10 do [k,combine(rem(A(k),B,X))] od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Il semble que le reste soit nul... Ce n'est pas une preuve, mais c'est une conjecture légitime. Démontrons-le en montrant que les racines de B sont aussi racines de A.
> solve(B,X);
![]()
![]() est bien définie sur l'ensemble
C
, c'est-à-dire qu'ici les racines sont
est bien définie sur l'ensemble
C
, c'est-à-dire qu'ici les racines sont
![]() et son conjugué.
et son conjugué.
> rac1:=exp(I*a);rac2:=exp(-I*a);
![]()
![]()
> `A(rac1)`:=subs(X=rac1,A(n));
![]()
Attention ! Les accents entourant A(rac1) signifie que c'est un nom de variable, et rien d'autre. Remarquez qu'il est bien choisi, mais il ne suffit pas de l'écrire pour évaluer A en rac1, puisque A n'est pas une fonction de X mais une expression dépendant de X.
> assume(n,integer);
> combine(`A(rac1)`);
![]()
> evalc(%);
![]()
> combine(%);
![]()
A étant à coefficients réels, le conjugué de rac1 est aussi racine de A. B étant scindé dans C, de degré 2, on a montré que toutes les racines de B sont racines de A et donc que B divise A.
> restart;
X.4
> P:=X^4-2*X^3+X^2-2*X+1;
![]()
> factor(P);
![]()
> fsolve(P);
![]()
Il semble y avoir deux racines réelles, et donc deux racines complexes conjuguées (coefficients réels)
> solve(P);
![]()
![]()
Ainsi, il y a quatre racines non exprimées... Essayons de les exprimer avec allvalues
> allvalues(RootOf(P));
![]()
Les racines semblent s'exprimer avec
![]()
> factor(P,sqrt(2));
![]()
Voilà qui est intéressant, mais pas complet puisqu'il
semble y avoir deux racines réelles. Les racines s'expriment avec
![]() .
.
> factor(P,sqrt(2*sqrt(2)-1));
![]()
Et voici la décomposition de Gauss de P
> restart;
X.5
> P:=X^(2*n)-n^2*X^(n+1)+2*(n^2-1)*X^n-n^2*X^(n-1)+1;
![]()
> Ptilde:=unapply(P,X);
![]()
> Ptilde(1);
![]()
> Ptildeprime:=D(Ptilde);
![]()
> Ptildeprime(1);
![]()
> simplify(%);
![]()
> Ptildeseconde:=D(Ptildeprime);
![]()
![]()
> Ptildeseconde(1);
![]()
> simplify(%);
![]()
> Ptilde3:=D(Ptildeseconde);
![]()
![]()
![]()
> Ptilde3(1);
![]()
![]()
> simplify(%);
![]()
> Ptilde4:=D(Ptilde3);
![]()
![]()
![]()
> Ptilde4(1);
![]()
![]()
> simplify(%);
![]()
Ainsi, 1 est racine d'ordre 4 si cette expression est non nulle
> solve(%);
![]()
On fait donc une étude directe pour les cas n=0 et n=1
> subs(n=0,P);
![]()
> subs(n=1,P);
![]()
Donc ces deux cas particuliers ne sont pas très intéressants, puisque P est le polynôme nul
> restart;
X.6
> P:=X^4+a*X^3+sqrt(3)*X^2+X+b;
![]()
> image:=subs(X=2+2*I,P);
![]()
> assume(a,real);assume(b,real);
> solve(image);
![]()
> solve({Re(image),Im(image)},{a,b});
![]()
> assign(%);
Ceci permet l'affectation des valeurs obtenues aux inconnues a et b
> 'a'=a;'b'=b;
![]()
![]()
> P;
![]()
> solve(P);
![]()
> evalf(-911+8*sqrt(3));
![]()
Ainsi il n'y a pas de racine réelle.
> factor(P);
![]()
Ceci est la décomposition de Gauss de P
> factor(P,{I,sqrt(-911+8*sqrt(3))});
![]()
Et cela la décomposition de d'Alembert.
> restart;
X.7
> P:=m->X^3+X^2+m*X+6;
![]()
Première méthode.
> s:=[solve(P(m),X)];
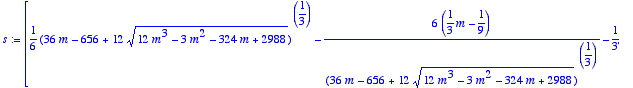
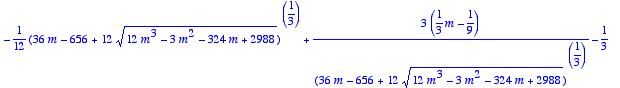

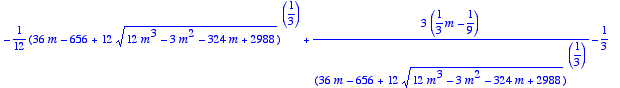
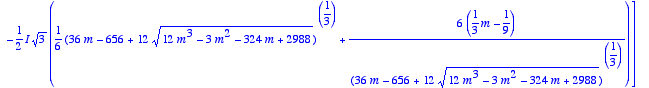
Même si le résultat n'est pas très esthétique, on a rangé toutes les racines dans une liste, et on va pouvoir les utiliser pour traduire les conditions et déterminerles valeurs de m qui conviennent.
> solve(s[1]+s[2]=s[1]*s[2],m);
![]()
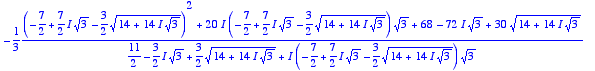
> evalf(%);
![]()
> solve(s[1]+s[3]=s[1]*s[3],m);
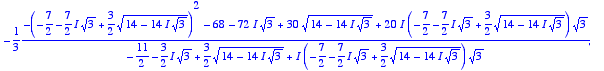
![]()
> evalf(%);
![]()
> solve(s[3]+s[2]=s[3]*s[2],m);
![]()
Vérifions que -4 et -9 conviennent.
> smoins9:=[solve(P(-9),X)];
![]()
> smoins9[3]+smoins9[2]-smoins9[3]*smoins9[2];
![]()
> simplify(%);
![]()
Et l'autre ?
> smoins4:=[solve(P(-4),X)];
![]()
> smoins4[3]+smoins4[2]-smoins4[3]*smoins4[2];
![]()
Deuxième méthode.
> syst:={p+c=-1,p+p*c=m,p*c=-6};
![]()
En utilisant les relations coefficients racines. où p est le produit des racines, abc les racines.
> solve(syst,{p,c,m});
![]()
On retrouve le même résultat. Trouvons les racines a et b correspondantes
> solve({a+b=-3,a*b=-3},{a,b});
![]()
> allvalues(%);
![]()
> solve({a+b=2,a*b=2},{a,b});
![]()
> allvalues(%);
![]()
Troisième méthode.
> Ptilde:=unapply(P(m),X);
![]()
![]()
> solve({Ptilde(a),Ptilde(b),a+b=a*b},{a,b,m});
![]()
![]()
Et on a directement le résultat. C'est un peu plus élégant que la première méthode...