Colle d'informatique IX

> restart;

Exercice IX.1

> f:=x->sin(x)/x;

> f(0);

Error, (in f) division by zero

> f(0):=limit(f(x),x=0);

> f(0);

> f(Pi);

> plot(f,-3*Pi..3*Pi);

Dérivabilité en 0

> limit((f(x)-f(0))/(x-0),x=0);

Donc f est dérivable en 0, de dérivée nulle.

Question subsidiaire : Peut-on appliquer le théorème du prolongement de la dérivée des fonctions continues ?

> g:=x->x*sin(1/x);

> g(0):=limit(g(x),x=0);

> plot(g(x),x=-0.1..0.1);

> restart;

Exercice IX.2

On utilise pour f une fonction de deux variables, ce qui facilitera le changement de a.

> f:=(a,x)->(x^2+a*x-3)*exp(1/x)/(1+x);

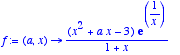
Tracé de quelques courbes .

Première méthode, celle qu'il faut utiliser.

> plot({seq(f(k,x),k=-10..10)},x=-4..4,-25..25,discont=true);

Seconde méthode, si on préfère des couleurs plus homogènes.

> for k from -10 to 10 do
A||k:=plot(f(k,x),x=-4..4,-25..25,
color=COLOR(RGB,(k/3+3)/10,(k/3+4)/10,(k/3+5)/10),discont=true);
od:

> with(plots):

Warning, the name changecoords has 
been redefined

> display([seq(A||k,k=-10..10)]);

Étude des asymptotes éventuelles .

En -1 . f admet une limite infinie en -1, sauf si 1+x divise , c'est-à-dire si le reste dans la division euclidienne est nulle.

> rem(X^2-a*X-3,X+1,X);

Ainsi Ca admet une asymptote verticale d'équation x=-1, sauf pour a=2 où f est prolongeable par continuité en -1.

En 0 . À gauche, f(x)->0. À droite f(x)->-infty, donc la courbe admet une demi-asymptote d'équation x=0

En +infty .On cherche à écrire avec en +infty.
On commence par chercher qui est la limite, si elle existe, de .

> limit(f(a,x)/x,x=infinity);

On cherche alors une limite finie à

> limit(f(a,x)-x,x=infinity);

Il suit alors que f(x)-x-a->0 en +infty, donc que la droite d'équation y=x+a est asymptote à Ca en +infty.

En -infty . L'étude est strictement analogue à celle précédente.

> limit(f(a,x)/x,x=-infinity);

> limit(f(a,x)-x,x=-infinity);

Même asymptote en -infty.

Recherche de Ca passant par M(xo,yo) .

On commence par exclure certaines valeurs évidemment impossible pour (xo,yo). Si xo=0 ou xo=-1, le problème n'aura pas de solution.

> solve(f(a,x)=y,a);

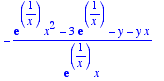
Le problème admet donc une unique solution. Il existe pour tout point M(xo,yo) un unique a tel que Ca passe par M.

Recherche de la courbe passant par M(1,15) .

> b:=subs({x=1,y=15},%);

> evalf(b);

Recherche du maximum relatif positif .

> plot(f(b,x),x=0.2..3,-1..30);

> diff(f(b,x),x);

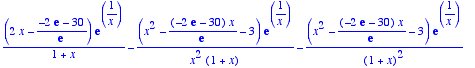
> normal(%);

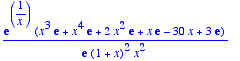
> s:=solve(%);

> seq(evalf(s[k]),k=1..4);

Il y a donc deux valeurs de x où la dérivée s'annule. Vu le graphe, c'est la plus petite qui correspond au maximum relatif, la plus grande correspondant à un minimum. Une valeur approchée du maximum est donc

> evalf(f(b,evalf(s[1])));

Si l'on veut vérifier que c'est un maximum, on peut montrer que la dérivée seconde de f est négative en s[1]

> fff:=diff(f(b,x),x,x):

> subs(x=evalf(s[1]),fff):

> evalf(%);

D'où la conclusion.

> restart;

Exercice IX.3

Définition de f

> f:=x->(x^2+x+1)*exp(1)^((x-1)/x)/(x);

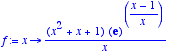
> # f est définie sur R*

Limites

> Limit('f(x)',x=-infinity)=limit(f(x),x=-infinity);

> Limit('f(x)',x=+infinity)=limit(f(x),x=+infinity);

> Limit('f(x)',x=0)=limit(f(x),x=0);

> Limit('f(x)',x=0,right)=limit(f(x),x=0,right);

> Limit('f(x)',x=0,left)=limit(f(x),x=0,left);

Branches infinies

Il y a une asymptote verticale d'équation x=0 ; la courbe se situe à gauche de cette asymptote.

On recherche une direction asymptotique en étudiant l'existence d'une limite au rapport f(x)/x. S'il y a une limite a, on cherche une limite à f(x)-x. Si on obtient b, alors f(x)-(ax+b) tend vers 0 donc la droite d'équation y=ax+b est asymptote à la courbe. La position de la courbe par rapport à son asymptote est donnée par le signe de f(x)-(ax+b).

> Limit('f(x)/x',x=+infinity)=limit(f(x)/x,x=+infinity);

> Limit('f(x)-exp(1)*x',x=+infinity)=limit(f(x)-exp(1)*x,x=+infinity);

> Limit('f(x)/x',x=-infinity)=limit(f(x)/x,x=-infinity);

> Limit('f(x)-exp(1)*x',x=-infinity)=limit(f(x)-exp(1)*x,x=-infinity);

> solve(f(x)-exp(1)*x,x);

> evalf(%);

Étude en 0

On a déjà déterminé la limite à droite en 0, qui nous permet de prolonger f par continuité à droite en 0 en posant :

> f(0):=0;

On étudie alors la dérivabilité à droite en 0

> Limit('(f(x)-f(0))/(x-0)',x=0,right)=limit('(f(x)-f(0))/(x-0)',x=0,right);

f ainsi prolongée est donc dérivable à droite en 0 et sa courbe admet une demi-tangente horizontale.

Variations de f

> df:=D(f);

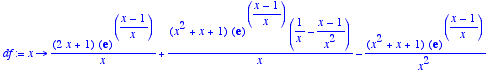
> df:=unapply(simplify(df(x)),x);

> solve(df(x)>0,x);

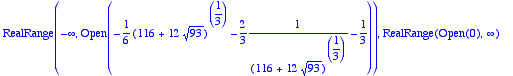
> alpha:=fsolve(df(x),x);

Ainsi, les variations de f sont les suivantes :

-infinity / f(alpha) \ 0 / infinity

Représentation graphique de f . Il y a plusieurs façons de faire ; j'aime utiliser display

> with (plots):

> asymptote1:=plot(exp(1)*x,x=-3..3,color=green):

> asymptote2:=implicitplot(x=0,x=-3..3,y=-15..0,color=green):

> tangente1:=plot([[0,0],[.3,0]],color=green):

> tangente2:=plot([[alpha-.3,f(alpha)],[alpha+.3,f(alpha)]],color=green):

> courbe:=plot(f(x),x=-3..3,y=-15..5,color=red):

> display(courbe,tangente1, tangente2,asymptote1,asymptote2);

Calcul de l'aire

Attention, entre 0 et 2, la courbe n'est pas située au dessus ou en dessous de l'asymptote. Il faut donc bien calculer l'intégrale de la valeur absolue de la différence.

> aire:=int(abs(f(x)-exp(1)*x),x=0..2);

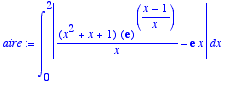
> 'aire'=evalf(aire);

> restart;

Exercice IX.4

Définition de g

> (-1)^(1/3);

> evalf(%);

> h:=x->(x^3-4*x^2+5*x)^(1/3);

> h(-1);

> evalf(%);

Il faut donc prendre des précautions...

> solve(x^3-4*x^2+5*x>0,x);

On sait donc définir g sans ambiguité sur R+. On la définit sur R- à partir de la définition sur R+ en utilisant l'imparité de y->y^(1/3)

> g:=x->piecewise(x>0,(x^3-4*x^2+5*x)^(1/3),x<0,-(-(x^3-4*x^2+5*x))^(1/3));

> g(-1);

> evalf(%);

Une autre méthode, presque équivalente, consiste à définir g en posant :

> #g:=x->piecewise(x>0,exp(1/3*ln(x^3-4*x^2+5*x)),x<0,-exp(1/3*ln(abs(x^3-4*x^2+5*x))));

Variations de g

> dg:=D(g);

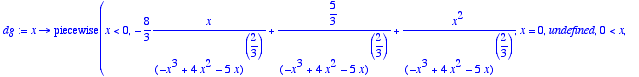
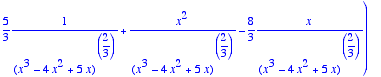
> solve(dg(x)>0,x);

D'où les variations de g

Étude en 0

> Limit('g(x)',x=0)=limit('g(x)',x=0);

> Limit('(g(x)-g(0))/(x-0)',x=0)=limit('(g(x)-g(0))/(x-0)',x=0);

g n'est donc pas dérivable en 0, mais sa courbe admet une tangente verticale.

Branches infinies

On recherche une direction asymptotique en étudiant l'existence d'une limite au rapport f(x)/x. S'il y a une limite a, on cherche une limite à f(x)-x. Si on obtient b, alors f(x)-(ax+b) tend vers 0 donc la droite d'équation y=ax+b est asymptote à la courbe. La position de la courbe par rapport à son asymptote est donnée par le signe de f(x)-(ax+b).

> Limit('g(x)/x',x=infinity)=limit('g(x)/x',x=infinity);

> Limit('g(x)-x',x=infinity)=limit('g(x)-x',x=infinity);

Ainsi, la droite d'équation y=x-4/3 est asymptote à la courbe au voisinage de +infinity

> Limit('g(x)/x',x=-infinity)=limit('g(x)/x',x=-infinity);

> Limit('g(x)-x',x=-infinity)=limit('g(x)-x',x=-infinity);

Même résulat en -infinity

Pour obtenir le signe de g(x)-x+4/3, voyons si son inverse a une limite en +/- infinity

> limit(1/(g(x)-x+4/3),x=infinity);

Donc g(x)-x+4/3 est négatif au voisinage de +infinity, la courbe est en dessous de son asymptote.

> limit(1/(g(x)-x+4/3),x=-infinity);

Donc g(x)-x+4/3 est positif au voisinage de -infinity, la courbe est au dessus de son asymptote.

Représentation graphique

> plot(g);

> with(plots):

Warning, the name changecoords has 
been redefined

> asymptote:=plot(x-4/3,x=-1..3,colour=green):

> t0:=plot([[0,.3],[0,-.3]],thickness=3,colour=green):

> t1:=plot([[1-.3,g(1)],[1+.3,g(1)]],thickness=3,colour=green):

> `t5/3`:=plot([[5/3-.3,g(5/3)],[5/3+.3,g(5/3)]],thickness=3,colour=green):

> courbe:=plot(g(x),x=-1..3,colour=red):

> display(courbe,t0,t1,`t5/3`,asymptote);

>