Exercices du chapitre VIII

> restart;

VII.1

Première méthode, récursive

> suite:=proc(n::integer)
option remember:
if n=0
then [1,sqrt(2)]
else [sqrt(op(1,suite(n-1))*op(2,suite(n-1))),
(op(1,suite(n-1))+op(2,suite(n-1)))/2]
fi:
end:

> suite(0);

> suite(1);

> evalf(suite(1));

Seconde méthode, itérative

> suite2:=proc(n::integer)
local k,a,b,c,d:
a:=1:b:=sqrt(2):
for k to n
# Au rang k, a représente uk-1, b vk-1, c uk et d vk
do c:=sqrt(a*b):
d:=(a+b)/2:
# On remplace alors a et b pour qu'elles représentes uk et vk
a:=c:
b:=d:
od:
[a,b]: # C'est la dernière expression évaluée qui sera renvoyée par suite2
end:

> suite2(0);

> suite2(1);

> evalf(suite2(1));

Vitesse de convergence

On pourrait utiliser les procédures précédentes, mais cela sera couteux en temps puisqu'il faudra à chaque fois recalculer tous les termes de la suite. Seule la procédure récursive, avec l'option remember peut ici se justifier.

> vitesse:=proc(epsilon::positive)
local k,a,b,c,d:
Digits:=floor(evalf((-ln(epsilon)/ln(10))))+3: # Permet de fixer le nombre de décimale pour dépasser de 2 chiffres la précision attendue (1 chiffre après la virgule et -log(epsilon)+2 après la virgule)
a:=1:b:=sqrt(2):
for k while is(abs(b-a)>epsilon)
do
c:=sqrt(a*b): # On travaille quand même par valeurs exactes pour ne pas cumuler les erreurs
d:=(a+b)/2:
a:=c:
b:=d:
od:
[evalf((a+b)/2),k]:
end:

> vitesse(10^(-30));

Avec l'intégrale

> J:=2/Pi*Int(1/sqrt(1-t^4),t=0..1);

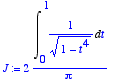
> for k to 5 do evalf(op(1,suite(k))*J); od;

On peut donc conjecturer que le produit tend vers 1.

>

> restart;

VIII.2

1. Approche graphique

> f:=x->(1+x^2)/2:

> with(plots):

Warning, the name changecoords has 
been redefined

> F:=plot(f,-0.1..1.1,-0.1..1.1,colour=red): X:=plot(x->x,-0.1..1.1,-0.1..1.1,colour=blue):

> display([F,X]);

Les coordonnées recherchées sont

> u0:=0:u:=n->(f@@n)(u0):

> L:=[u(0),0]:

> for k to 10 do L:=L,[u(k-1),u(k)],[u(k),u(k)] od:

> L:=[L]:

> U:=plot(L,colour=green):

> display([F,X,U]);

>

2. Étude précise

Si la suite converge, par passage à la limite dans l'égalité , en utilisant la continuité de en la limite , elle converge vers tel que . On résout donc cette équation.

> solve(f(x)=x,x);

Il y a donc une unique racine (double) à cette équation. Si la suite converge, c'est vers .

>

Pour étudier le signe de , on cherche d'abord sa forme factorisée.

> factor(f(x)-x);

C'est un carré, donc on a pour tout ,

La suite est croissante. Par récurrence immédiate, comme et est croissante, alors elle est majorée par 1 donc convergente, vers 1 d'après 2a.

>

> restart;

VIII.3

> visu:=proc(g::procedure,alpha::realcons,n::integer,I1::range,I2::range)
local u,L,k,F,G,H;
with(plots):
# Premiere methode
#u:=i->(g@@i)(alpha);
#L:=[[u(0),0]];
#for k to n
# do L:=[op(L),[u(k-1),u(k)],[u(k),u(k)]]
# end do;
# seconde methode
u:=alpha;L:=[[u,0]];
for k to n
do
L:=[op(L),[u,g(u)],[g(u),g(u)]];
u:=g(u);
end do;
F:=plot(x,x=I1,I2,color=green):
G:=plot(g,I1,I2,color=red):
H:=plot(L,I1,I2):
display([F,G,H]);
end:

> visu(x->(1+x^2)/2,0,10,-0.1..1.1,-0.1..1.1);

> visu(x->1-x^2,1/2,15,-1..2,-1..2);

> visu(x->1-x^2,-3/2,10,-2..1,-2..2);

> visu(cos,1/2,20,0..1,0..1);

> f:=x->(3*x-2)/(1-x):

> visu(f,1/2,10,-4..3,-6..4);

> visu(f,3/4,10,-4..3,-6..4);

Error, (in f) division by zero

Le problème vient du fait qu'avec cette valeur de , la suite n'est pas bien définie. Le terme n'est pas défini si . Pour chercher les valeurs interdites, on cherche les valeurs de telles que , c'est-à-dire si on note la dernière valeur interdite .

> v[0]:=1;

> for k to 10 do v[k]:=solve(f(x)=v[k-1],x) end do:

> seq(v[i],i=0..10);

> restart;

VIII.4

Définition des deux suites.

> u:=n->2*sqrt(n)-sum(1/sqrt(k),k=1..n);
v:=n->2*sqrt(n+1)-sum(1/sqrt(k),k=1..n);

Variations de v

> combine(v(n+1)-v(n));

> normal(%);

> numer(%);

Il faut comparer et . On va étudier le signe de la différence de leurs carrés.

> (2*sqrt((n+1)*(n+2)))^2-(3+2*n)^2;

> expand(%);

v est donc décroissante.

Variations de u

> combine(u(n+1)-u(n));

> normal(%);

La différence est du signe de

> (1+2*n)^2-4*n*(n+1);

> expand(%);

Donc u est croissante.

Limite de v-u

> v(n)-u(n);

> limit(%,n=infinity);

Les deux suites sont bien adjacentes.

> with(plottools):with(plots):

Warning, the name changecoords has 
been redefined

> UU:=[]:VV:=[]:
for i to 100 do
U||i:=point([i,u(i)], color=blue);
UU:=[op(UU),U||i];
V||i:=point([i,v(i)], color=green);
VV:=[op(VV),V||i];
od:

> display([op(UU),op(VV)]);

> limit(u(n),n=infinity);

> evalf(%);

> limit(v(n),n=infinity);

Tout va bien...