Chapitre III
Première partie
> restart;
1. Séquences
> 3,4,5;
![]()
> s1:=a,b,c; s2:=(d,e);
![]()
![]()
> sequence:=s1,s2,f,g,h;
![]()
> seqvide:=NULL; # la séquence vide.
![]()
> sequence[1],sequence[8]; sequence[9];
![]()
Error, invalid subscript selector
> sequence[2]:=x;
Error, cannot assign to an expression sequence
> sequence:=sequence[1],x,sequence[3..8];
![]()
>
> seq(2^i,i=1..10);
![]()
> 2^i $ i=1..10;
![]()
> j $ 5;
![]()
> seq(k^2,k=1..n);
Error, unable to execute seq
> k^2 $ k=1..n;
![]()
> subs(n=5,%);
![]()
> eval(%);
![]()
> restart;
2. Ensembles
> {3,4,5};
![]()
> {5,4,3};
![]()
> {a,d,d,b,f,b,e,c,c};
![]()
> {seq(1/k,k=1..10)};
![]()
> ensvide:={};
![]()
Autre ensemble vide
> ensvide2:={NULL};
![]()
> ens1:={1,2,3,4,5};
![]()
> ens2:={seq(2*k,k=0..3)};
![]()
> "Réunion"=ens1 union ens2;
![]()
> Intersection:=ens1 intersect ens2;
![]()
> `Différence de ens1 et ens2`:=ens1 minus ens2;
![]()
> op(ens1);
![]()
> nops(ens2);
![]()
> restart;
3. Listes
> li1:=[Alain, Bernard, Céline];
![]()
> li1[3];
![]()
> li2:=[Daniel,Élise];
![]()
> seq3:=Frédérick, Guillaume;
![]()
> li3:=[seq3];
![]()
> `Mauvaise liste`:=li1,li2,li3;
![]()
> `Bonne liste`:=[op(li1),op(li2),op(li3)];
![]()
> `Pour la frime`:=[seq(op(li||k),k=1..3)];
![]()
> li1[2]:=Bertrand; # Méthode à éviter.
![]()
> li1;
![]()
> li1:=subsop(2=Bruno,li1); # C'est la bonne méthode.
![]()
>
> restart;
>
> subs(x=1,y=2,3*x+2,5*y+4);
Error, wrong number (or type) of parameters in function subs
> subs(x=1,y=2,[3*x+2,5*y+4]);
![]()
>
Deuxième Partie
> restart;
1. Définition d'un fonction
Opérateur flèche
> restart;
> f:=x->2*x^2+3;
![]()
> f(5);
![]()
> f(a+b);
![]()
> expand(%);
![]()
> g:=(x,y)->cos(x-y^2);
![]()
> g(Pi,sqrt(3*Pi)/2);
![]()
Fonctions définies par morceaux
> f:=x->piecewise(x<0,-x^2+1,x<1,-x+1,x^2-1);
![]()
> plot(f,-2..2);
![[Maple Plot]](images/03cours_exos46.gif)
Utilisation de unapply
> expr:=3*x+4;
![]()
> f:=x->expr;
![]()
> f(2);
![]()
> f:=unapply(expr,x);
![]()
> f(2);
![]()
>
> restart;
> L:=[seq(x->x^k,k=1..4)];
![]()
> L[2];
![]()
> L1:=[seq(subs(n=k,x->x^n),k=1..4)];
![]()
> L2:=[seq(unapply(x^k,x),k=1..4)];
![]()
> L1[3](t);L2[3](t);
![]()
![]()
Utilisation des procédures
>
signe:=proc(x::realcons)
if x>0 then "+"
elif x<0 then "-"
else "0"
fi
end;
![]()
> signe(3);
![]()
> signe(-2);
![]()
> signe(0);
![]()
> signe((a+b)^2-a^2-b^2-2*a*b);
Error, signe expects its 1st argument, x, to be of type realcons, but received (a+b)^2-a^2-b^2-2*a*b
> signe(-Pi);
Error, (in signe) cannot evaluate boolean: Pi < 0
2. Opérations sur les fonctions
Composition
> restart;
> g:=x->x+Pi/2;
![]()
> f:=cos@g;
![]()
> simplify(f(x));
![]()
> h:=sin@(g@@4);
![]()
> simplify(h(x));
![]()
Tracés de représentations graphiques
Avec des fonctions
> plot(sin);
![[Maple Plot]](images/03cours_exos67.gif)
> plot(x->x^2*sin(1/x),-0.1..0.1,thickness=2);
![[Maple Plot]](images/03cours_exos68.gif)
> plot(t->3*a*ln(t),0..1,thickness=2);
![[Maple Plot]](images/03cours_exos69.gif)
> H:=x->1/(1-x^2+I*x/Q);
![]()
> Hnum:=unapply(subs(Q=1,H(x)),x);
![]()
> G:=abs@Hnum;
![]()
> plot(G,0..10,thickness=2);
![[Maple Plot]](images/03cours_exos73.gif)
> with(plots):
Warning, the name changecoords has been redefined
> semilogplot(20*log[10]@G,0.1..10,title="Diagramme de Bode",thickness=2);
![[Maple Plot]](images/03cours_exos74.gif)
Avec des expressions
> plot(cos(x),x);
![[Maple Plot]](images/03cours_exos75.gif)
> P:=a*x^2+b*x+c;
![]()
> Pnum:=subs(a=1,b=-2,c=4,P);
![]()
> plot(Pnum,x=-5..5);
![[Maple Plot]](images/03cours_exos78.gif)
Représentation simultanée de plusieurs graphes
> plot({cos(x),1-x^2/2},x=-Pi..Pi,thickness=2);
![[Maple Plot]](images/03cours_exos79.gif)
> approx:=seq(sum(x^k/k!,k=0..n),n=1..5);
![]()
> plot([exp(x),approx],x=-3..3,color=[red,blue $ 5],thickness=2);
![[Maple Plot]](images/03cours_exos81.gif)
Représentation simultanée de plusieurs graphes
> restart;with(plots):
Warning, the name changecoords has been redefined
> g1:=plot(cos(x),x=-2*Pi..2*Pi,color=magenta,thickness=2):
> g2:=plot(sin(x),x=-2*Pi..2*Pi,color=blue,thickness=2):
> g3:=plot(tan(x),x=-2*Pi..2*Pi,-3..3,color=green,discont=true,thickness=2):
> display([g1,g2,g3],title="Principales fonctions trigonométriques");
![[Maple Plot]](images/03cours_exos82.gif)
Tracé de lignes brisées
> plot([[0,0],[1,3],[4,3],[0,0]]);
![[Maple Plot]](images/03cours_exos83.gif)
> plot([[0,0],[2,2],[0,2],[1,3],[2,2],[2,0],[0,2],[0,0],[2,0]],scaling=constrained,axes=none,color=aquamarine);
![[Maple Plot]](images/03cours_exos84.gif)
Utilisation de map
> restart;
> f:=t->t^2;
![]()
> map(f,a*x+b);
![]()
> map(f,t*(a+b));
![]()
> map(f,[seq(y||i,i=1..5)]);
![]()
Exercices du chapitre III
> restart;
Exercice V.1
> assume(a,real);assume(b,real);z:=a+I*b;
![]()
> p:=expand(z*z+conjugate(z)+I*z);
![]()
> sol:=solve({Re(p),Im(p)},{a,b});assign(sol);
![]()
D'où les solutions complexes, que l'on va représenter :
> allvalues(z);pts:=allvalues([a,b]);
![]()
![]()
On laisse par ce procédé la solution nulle ... Rajoutons-la, puis représentons le triangle introduit par l'énoncé :
> for i to 2 do sol||i:=op(i,[pts]) od;sol||0:=[0,0];
![]()
![]()
![]()
> with(plots):plot([seq(sol||i,i=0..2),sol||0],scaling=constrained);
![[Maple Plot]](images/03cours_exos97.gif)
Ce triangle semble effectivement rectangle en O. On le vérifie à l'aide d'un produit scalaire :
> with(linalg):simplify(dotprod(sol1,sol2));
Warning, the protected names norm and trace have been redefined and unprotected
![]()
On peut aussi le vérifier en utilisant les propriétés des complexes
> solcomplexe:=[allvalues(z)];
![]()
> rationalize(solcomplexe[1]/solcomplexe[2]);
![]()
> evalc(%);
![]()
Ainsi, on passe d'une solution à l'autre en multipliant par un imaginaire pur, c'est-à-dire que l'angle considéré est droit.
>
>
> restart;
Exercice V.2
> Z:=z^2/(2*z+3*I);
![]()
> assume(x,real):assume(y,real):Z:=subs(z=x+I*y,Z);
![]()
Z est imaginaire pur si et seulement si Z+conjugate(Z)=0. On utilise normalize pour supprimer les imaginaires du dénominateur.
> rationalize(Z+conjugate(Z));
![]()
> eq:=numer(%);
![]()
Ainsi Z est imaginaire pur si et ssi x=0 ou x^2+y^2+3y=0. On peut reconnaître les éléments caractéristiques du cercle et de la droite, ou les représenter directement à l'aide d'implicitplot
> with(plots):
Warning, the name changecoords has been redefined
> implicitplot(eq,x=-2..2,y=-4..1,numpoints=1000,thickness=2,scaling=constrained);
![[Maple Plot]](images/03cours_exos106.gif)
>
> restart;
Exercice V.3
> f:=z->(z-2*I)/(z+I);
![]()
> solve(f(z)=y,z);
![]()
Ainsi, pour tout y<>1, l'équation f(z)=y admet une unique solution, donc tout y de C\{1} admet un unique antécédent qui est dans C\{-i}. D'où le résultat.
> assume(x,real):assume(y,real):assume(u,real):assume(v,real):
On a immédiatement
> sys:={u=Re(rationalize(f(x+I*y))),v=Im(rationalize(f(x+I*y)))};
![]()
Pour obtenir x et y en fonction de u et v, il faut inverser les formules précédentes, c'est-à-dire résoudre le système précédent en considérant x et y comme inconnues.
> solve(sys,{x,y});
![]()
Étudions le signe de |f(z)|^2-1, et trouvons à quelle condition celui-ci est négatif.
> test:=(abs(f(x+I*y))^2-1);
![]()
> test:=normal(test);
![]()
Il est clair que le dénominateur est positif (somme de deux carrés), donc test<0 si et ssi 2y-1>0, c'est-à-dire y>1/2, ce qu'il fallait démontrer.
>
> restart;
Exercice V.4
> f:=z->(z+1/z)/2;
![]()
Notons C ce cercle. Alors C est l'ensemble des Reit, avec t dans [0,2Pi]
> assume(t,real);assume(R,real);Image1:=f(R*exp(I*t));
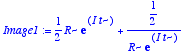
> Image1:=convert(Image1,trig);
![]()
> Image1:=simplify(expand(rationalize(Image1)));
![]()
> x:=Re(Image1);y:=Im(Image1);
![]()
![]()
> xnum:=subs(R=3,x);ynum:=subs(R=3,y);
![]()
![]()
On reconnaît l'équation paramétrique d'une ellipse.
> plot([xnum,ynum,t=0..2*Pi],scaling=constrained);
![[Maple Plot]](images/03cours_exos121.gif)
>
Notons D la demi-droite. C'est l'ensemble des teitheta avec t dans [0,+infty[
> assume(t,real);assume(theta,real); Image2:=f(t*exp(I*theta));
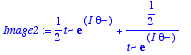
> Image2:=convert(Image2,trig);
![]()
> Image2:=simplify(expand(rationalize(Image2)));
![]()
> x:=Re(Image2);y:=Im(Image2);
![]()
![]()
> xnum:=subs(theta=3*Pi/8,x);ynum:=subs(theta=3*Pi/8,y);
![]()
![]()
> plot([xnum,ynum,t=0.2..5],scaling=constrained);
![[Maple Plot]](images/03cours_exos129.gif)
>
>